Initial stress

In slender structures the axial force in a 1D member may have a big effect on the stiffness of the overall structure and the stiffness of its parts. In general, tensile force increases the stiffness and compression force reduces the stiffness of the structure.

It is possible to define initial pre-stressing forces in individual 1D members. These forces are considered constant along the whole 1D member.

The effect of initial pre-stressing can be taken into account in ALL or NONE nonlinear combination. In addition, also buckling calculation and dynamic free vibration analysis may take account of initial pre-stressing.

When inserted into the model, a 1D member with this type of nonlinearity is marked by the following symbol (remember that in order to see the symbol, view parameters must be adjusted to show model data).

Parameters

Normal force

Specifies the initial axial force applied in the 1D member.

A bit of theory

Initial stress can be defined in two forms: either (i) as a load case, or nonlinear combination, result, or (ii) as a given initial axial force in certain elements. For the second approach, the forces are transformed into shrinkage or elongation of 1D members. That situation is analysed in order to obtain a balanced solution. The result of this calculation is then treated the same way as in the first approach.

In principle, the initial stress is viewed as a result of loading that was applied before the given load case or nonlinear combination. The geometry defined by the user is, however, assumed to be the same as before this initial loading. The solution that is used as the initial one is thus obtained on the defined (unchanged) geometry. The procedure that follows depends on (i) whether a linear or nonlinear calculation is used and (ii) whether we deal with the first, second or third order (the first order is a geometrically linear calculation, the second order can be found in the dialogue under the option Timoshenko and the third order under the name Newton-Raphson).

1. Linear calculation

The initial stress is used only to determine the impact of the stress-state on the stiffness of the structure (termed geometrical stiffness matrix). It is advantageous to use e.g. the stress-state resulting from the permanent load for the analysis of all load cases defined on the structure or for the dynamic analysis. With regard to the fact that the right-hand side of the equation remains unchanged, the principle of superposition can be applied (together with the possibility to calculate the critical combinations) and the significant effect of the geometrical nonlinearity can be taken into account. Neither the initial stress nor the initial deformations are added to the results (otherwise the combinations could not be created).

2. Nonlinear calculation

As a rule valid for all kinds of nonlinear calculations, the results of a nonlinear solution include also the deformations and stresses resulting from the initial loading (i.e. not just the effect of the stress-state on the stiffness of the structure).

a) The first and second order

The initial stress is used to modify the stiffness of the structure. The calculation is carried out with the load of a given nonlinear combination and the results of the initial load case are then added to the obtained results, including deformations and reactions.

b) The third order

It is necessary to take into account the way by which the initial loading was calculated. The procedure that is used to process the initial state depends on whether the initial state was calculated by the third order or not.

What is important is whether the equilibrium was calculated on the original or deformed geometry.

The initial shape must correspond to the one for which the equilibrium was calculated.

aa) The initial state was calculated by the 1st or 2nd order

The initial stress is used for the geometrical stiffness in the calculation. The initial shape is not changed. After finishing the calculation, the initial deformation is added to the results of the nonlinear combination. It must be emphasised that this approach is not suitable especially for cable and membrane structures. In any case, it is always better to apply the third order to the determination of the initial state if the third order calculation is to be performed.

bb) The initial state was calculated by the 3rd order

The deformations from the initial state are added to the geometry, which means that the analysis is performed on a deformed structure. The initial loading is applied into the calculation as an old load (similarly to the analysis of construction stages). Once the calculation has been performed, it is necessary to add the initial deformations to the deformations of the analysed nonlinear combination, so that the user obtains, after adding these total deformations to the initial geometry of the structure, the final shape of the structure (he is not in fact aware that the calculation has been performed on a modified structure). The analysis of stresses in the third order calculation is similar to the analysis of construction stages.

Consequently, in all nonlinear calculations, unlike in the linear calculation, the result of the initial state is fully included into the results (including the initial deformations). In order to determine the detailed forces in 1D members, both (i) the final end-forces including the results of the initial load case and the (ii) the final load on 1D members (including the initial loading) are used.

Example

The initial stress may differ from beam to beam and is always considered constant along one particular beam.

The application is demonstrated on a following example.

The definition of an initial stress is made in a similar way as the compression-only property is adjusted for compression-only beams.

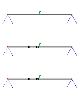
Let’s assume a simply supported beam with two pinned ends.

The first (top most) beam is a standard beam without any initial stress defined.

The second (the middle) one is subject to a compression axial force of 50kN (i.e. –50 kN).

The third (bottom most) beam is subject to a tensile axial force of 50kN (i.e. +50 kN).

All the variants are subject to the same external load: a vertical concentrated force.

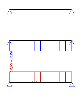
The definition may be easily verified on diagrams of calculated axial force.

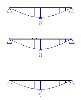
The last set of pictures then shows the effect of the initial stress on vertical displacement. The beam subject to an initial compression shows the biggest deformation.