Analysis of a haunch with reference to eccentric elements

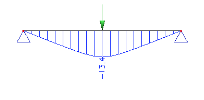
By default, a haunch is idealised by a set of finite elements that vary in cross-section from one element to another and whose middle axes lie in one line. This idealisation corresponds fully with a haunch whose midline is straight and whose both surfaces are inclined (see Fig.).

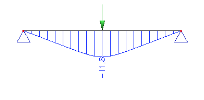
In practice, however, one more often comes across a haunch with an aligned top or bottom surface (see Fig.).

In this second case, the midline of the beam is not a straight line but it resembles an arch. This produces an arch effect whose practical outcome is shown in the following set of pictures.

Let’s assume a simply supported beam with both ends pinned subjected to a concentrated force load located in the middle of the span.

The first finite element model (option "Generate eccentric elements on haunches, arbitrary beams" is OFF) gives displacement in the middle of the span equal to 13.4 mm.

If however, the option "Generate eccentric elements on haunches, arbitrary beams" is set ON, the result displacement measured in the same place is only 11.8 mm.

The difference is about 12 percent, which is quite significant.

One must be aware of a "side effect" of the latter approach. Consider once again our model example of a beam pinned on both ends. None of the hinges provides for a horizontal movement. The midline of the beam is an "arch-like" curve and this means that under given loading conditions axial force appears in the beam. As there is an eccentricity introduced into the model, there will be a bending moment in both end-points of the beam. The moment in the support will be equal to the product of calculated axial force and introduced eccentricity.

Axial force diagram looks like:

The depth of the haunch on its left-most side is equal to 1 metre. An easy calculation gives:

axial force * eccentricity equal to a half of the haunch depth = bending moment

(88) * (1/2 * 1.0) = 44