Analysis of a haunch versus mesh size
For haunch, the division of members into finite elements may play a significant role.
A haunch is an element of a variable cross-section. A 1D finite element used in SCIA Engineer, on the other hand, is an element of a constant cross-section. Therefore, the effect of the varying cross-section (most often of a varying depth of the cross-section) must be modelled by means of a finer finite element mesh.
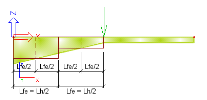
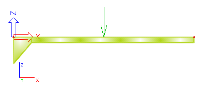
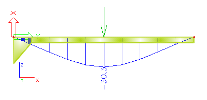
The practical application is shown in the figure below.
The example shows a beam with a haunch stretching over a half of total beam length. Let’s assume that the division is set to "2 finite elements per a haunch". When the finite element mesh is being generated, each haunch is cut into the specified number of segments, i.e. into two segments in our example. Then, the dimensions of the cross-section in the middle of each of the segments are calculated. These dimensions are used to create an ideal cross-section of the corresponding finite element.
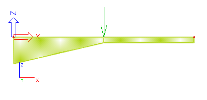
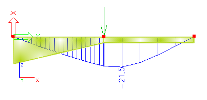
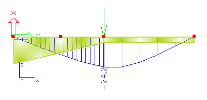
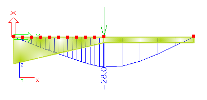
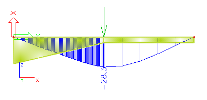
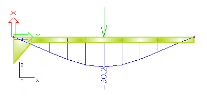
The approach presented above means, that the higher the number of finite elements per a haunch is, the more realistic model of the haunch is obtained. On the other hand, from a practical point of view, it is not necessary to generate "overprecise" haunches. The gain in the numerical precision is not in proportion to the number of finite elements per haunch. There is a big difference in the precision of results for very course division and for considerably fine division. But the difference between the considerably fine division and extremely fine division is almost negligible. Compare the deformation calculated for division equal to 1, 2, 10 and 50 finite elements per haunch.
|
analysed beam |
|
|
1 FE per haunch (deformation given in millimetres) |
|
|
2 FEs per haunch (deformation given in millimetres) |
|
|
10 FEs per haunch (deformation given in millimetres) |
|
|
50 FEs per haunch (deformation given in millimetres) |
What’s more, the above stated facts are not applicable to all cases. What also influences the "reasonable" division is the relative length of the haunch. If the haunch extends along a considerably smaller part of the beam, the required number of finite elements per haunch decreases. See another example.
|
analysed beam |
|
|
1 FE per haunch (deformation given in millimetres) |
|
|
10 FEs per haunch (deformation given in millimetres) |