Natural vibration analysis versus mesh size

A natural vibration calculation is not a very complex problem. Nevertheless, one important point should be emphasised. In order to obtain greater number of eigenmodes (and natural frequencies as well) finer mesh of finite elements must be used. This must be fulfilled for both beam and plane elements. The effect of mesh density will be demonstrated on a simple planar frame.

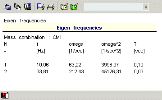
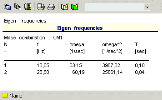
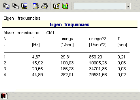
The frame consists of three beam members. The default mesh division (i.e. the generation of a single finite element per a beam) would lead to a numerical model containing there are three finite elements and four nodes from which two nodes are supported. The structure has six degrees of freedom if solved as a 2D problem (Frame XZ project). The degrees of freedom are a vertical translation, a horizontal translation and a rotation in each of the corners. Therefore, six eigenmodes at most may be calculated for such a structure. If more eigenmodes than degrees of freedom are required a warning is issued and the calculation is terminated. Moreover, the calculation is abnormally terminated even if six eigenmodes are required since the algorithm works internally with increased number of eigenmodes. The fact that the higher eigenmodes are not calculated in our example has a significant advantage. If they were calculated they would show a significant numerical error caused by the coarse finite element mesh. Thus, the calculated results for the higher eigenmodes would be practically unusable. As a result, if higher natural frequencies should be calculated, finer mesh must be generated for the structure. The comparison of results for both coarse and fine finite element mesh is shown below. It can be clearly seen that while the first eigenmode is almost identical for both variants the other one differs.

coarse mesh 1 FE per beam)
finer mesh 4 FEs per beam)

For instance, the deflection of the horizontal beam is completely different due to the absence of the node (mass degree of freedom) in the middle of the span. The natural frequency of the frame with lower number of degrees of freedom is higher just due to a lack of mass degrees of freedom, i.e. due to smaller portion of inertia energy in the total deformation energy of the system. This error grows rapidly with an increasing frequency.

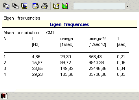
A similar result may be examined for another example. Now, let’s consider a two-storey frame:

The effect of the finite element size is now even more significant as one frequency has been skipped in the calculation performed for the single-element-per-beam division.

coarse mesh 1 FE per beam)
finer mesh 4 FEs per beam)