Validation of modal analysis: immobilized masses
Dynamic analysis troubleshooting > modal analysis > immobilized masses
Check for immobilized masses
Immobilized masses, such as an overall foundation slab or a very rigid basement, can cause a significant part of the mass of the structure to remain immobile under seismic excitation. An overall foundation slab is typically ticker than the average slab and covers the entire surface of a building, thus representing a quite important mass.
Because of the associated high values of stiffness, the modes associated to such masses usually have very high frequencies, which are out of the usual range of seismic action, and their mode shape has often little real physical meaning.
The presence of such immobilized masses in the model does not necessarily mean, that results are incorrect or invalid. However, it makes the application of standard validation criteria inconvenient at best.
Example
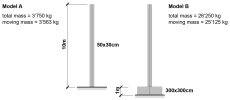
Consider the simple structure below, consisting of a single column. Model A represents the column alone directly on a fixed support. Model B represents the same column with its foundation block; in the second case, the fixed support is placed underneath the foundation block.
The masses of models A and B are very different. However, the first 3 modes obtained from modal analysis are identical for the column part of the model. On the other hand, relative modal mass values are very different.
| Model A | Model B | |||
|
|
|||
| Mode | f [Hz] | Wi/Wtot [%] | f [Hz] | Wi/Wtot [%] |
| 1 | 2.6 | 64.4 | 2.6 | 9.1 |
| 2 | 15.9 | 20.0 | 15.9 | 2.9 |
| 3 | 43.5 | 6.9 | 43.5 | 1.0 |
| Sum | 90.3 | 13.0 | ||
According to code criteria, model B with 3 modes is not sufficient for seismic analysis of the structure.
Only increasing the number of modes to meet the code criteria, it is necessary to compute at least 23 modes for model B:
| Model B | ||

|
||
| Mode | f [Hz] | Wi/Wtot [%] |
| 1 | 2.6 | 9.1 |
| 2 | 15.9 | 2.9 |
| 3 | 43.5 | 1.0 |
| 14 | 453 | 70.5 |
| 23 | 1350 | 8.9 |
| Sum | 92.4 | |
The next two significant modes for model B are listed in the table above. Although they exhibit important values of relative modal mass, these two modes are irrelevant for seismic behaviour:
- Their frequency is out of seismic frequency range. Typical seismic action frequency ranges up to 35 Hz. Actually, mode 3 is already out of that range.
- The corresponding mode shapes are essentially shear deformations within the foundation slab itself, which is quite unrealistic.
Essentially, such high-frequency modes should rather be considered as so-called rigid modes and submitted directly to ground acceleration, without any dynamic amplification due to structural vibrations.
Please note: in complex models, increasing the number of modes to reach 90% of relative modal mass can become prohibitive
Looking just at results in the column above the foundation, results are identical:
Results change, of course, at the bottom of the foundation when increasing the number of modes, but it is irrelevant here. Important is, that the results in the column do not change at all.
Also interesting to notice, the relative modal mass values obtained from model B for the first 3 modes are directly proportional to the value from model A, in the inverse proportion of moving masses. Multiplying relative modal masses form model B by that ratio gives values that are very close to the results of model A:
| Model A | Model B | ||

|

|
||
| Mode | Wi/Wtot [%] | Wi/Wtot [%] |
|
| 1 | 64.4 | 9.1 | 64.4 |
| 2 | 20.0 | 2.9 | 20.1 |
| 3 | 6.9 | 1.0 | 7.1 |
| Sum | 90.3 | 13.0 | 91.6 |
Immobilized, rigid masses do not affect the behaviour of the moving parts of the structure. This leads to the following conclusions:
- Immobilized, rigid masses can - should - be removed from the model
- keeping immobilized, rigid masses does not affect the results in the rest of the structure. Those results are correct. Only their validation is not directly possible according to code criteria such as the 90% relative modal mass rule. A simple ratio calculation might help estimating the validity.
Solutions
In case the 90% condition cannot be satisfied due to immobilized, rigid masses in the model, the following corrections can be applied, separately or combined depending on the case:
- Remove the immobilized masses from the model; most often, this concerns structural elements at and below the overturning reference level
- In case immobilized masses need to be taken into account, apply the method of residual mode to take rigid modes into account in the response of the structure (see "Seismic loading: Mass in the seismic analysis"). It's an approach that is both more correct from a theoretical point of view and less computationally intensive than increasing the number of computed modes.
- Increase the number of computed modes; this, however, is the correct approach as long as the added modes are relevant for the overall seismic behaviour of the structure.