Punching - Theory

Basis of calculation

Phenomenon of punching means a local shear failure around a concentrated load on a plate. The most common situations where the punching has to be considered is the region immediately surrounding a column in a flat ceiling plate or where column is supported on a foundation plate. The following problem types can be currently distinguished there: interior, edge and corner columns. Design of punching shear reinforcement is based on Re 6.4.5 from [1] DAfStb Guideline "Steel fibre reinforced concrete" together with clauses 6.4 and 9.4.3 in EN 1992-1-1: 2004 / AC:2014 + National Annexes. The calculation reveals either that the load-bearing capacity of the steel fibre reinforced concrete is sufficiently high or that specific amount of punching shear reinforcement is required. If the verification limits are exceeded, such a result is marked as not permissible. In that case, the user must change the model parameters or select a suitable design alternative.

Modelling

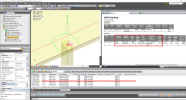
Places, where the punching design is calculated and results are available, can be defined automatically or manually (see Punching command). However, the final selection always contains just structural nodes, which fulfil the following criteria:

• node has the reference on a plate (=2D member) from steel fibre concrete material
• node has a reference on a columns below and /or above the plate (=1D member) or support in node
• node does not contain any further reference on beams or other columns

The described filtering of structural nodes is integrated to the design procedure and is run automatically. Up to the user is just specify which part of the model should be considered for that filtering (by choosing a specific selection type in command which respects to current activity).

Note: If manually defined selection contains structural nodes not applicable for punching at all, such nodes are removed from the selection and user is informed about that fact in the graphical window and preview.

Input data

All input data required by the punching design procedure are prepared from the model for each node automatically. User is able to check them all via Standard output. The input data cannot modify by user directly, since any additional data applicable on the node does not yet exist for the Punching design (be aware that punching data from Concrete Advanced service are not taken into account at all). However, most of inputs can be changed by updating the related parameters in model.

Note: Part of the preparation of input data is a check, whether a selected node can be successfully calculated for punching or some limitation is reached (for complete list see E/W/N). When node cannot be successfully calculated, the results are set to not available values (N/A) and final unity check of the design itself is set to the error value (as default UC=3.0). Explanation and possible solution of such cases is available through E/W/N system.

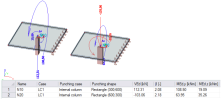
Punching load and area

The punching load and related loaded area are evaluated for each combination separately to properly consider which surface (side) of the plate is actually loaded. Key step is to determine the punching shear force, V_Ed, and based on its sign (respective direction) is decided about a governing column (the one punched through the plate). The loaded surface of the plate than lies on opposite side than the governing column. In addition to that, corresponding unbalanced bending moments M_Ed,y and M_Ed,z are registered as input for calculation of β-factor using a general formula. The evaluation of the punching load varies with selected approach for modelling the point-type support of the plate at a calculated node. Selected approach also determines what coordination system is taken as a referenced for the loaded area to be further used for the rest of punching design procedure. Two categories of point-type support of plates may be recognized in the model.

Punching load from support in node

First option is modelling plate with supports in nodes, where the loaded area of each node is derived according to a type of using support as follows:

• Standard support - square cross-section is assumed with the inputted size
• Column support - assigned cross-section is taken with inputted dimensions

For both types, the coordination system of the loaded area is determined from the coordination system of the node itself with just substitution of axes (x=y and y=z). When the support is rotated around its z-axis, this rotation is taken into account and the loaded area is rotated as well. The punching shear force V_Ed is taken as component R_z of the reaction in the support including its sign (which is positive when the direction of R_z is same like the direction of global z-axis). The unbalanced moments are derived from moment reactions M_x and M_y, which again are just transformed to the coordination system of the loaded area and presented in absolute values.

Punching load from columns

Second possibility of point-type support of plate is direct modelling of columns above and below the plate as connected 1D members. The loaded area is taken same as shape of cross-section from the governing column (punched through the plate). The shear force, V_Ed, is calculated as a resultant of columns normal (axial) forces acting perpendicularly on the plate. For calculation of the resultant is used the following convention of direction of normal force based on its sign:

• compressive (negative sign) - means the force in direction from the column into the plate (punching)
• tension (positive sign) - means the force in direction from the plate into the column (pulling)

In case of a single column connected to the plate, the shear force is directly the normal force from the end section of the column on side relating to the node. If both columns below and above the plate are modelled, the shear force V_Ed is taken as the resultant as follows. If both normal forces are compression (with same sign), just differential force is accounted as shear force else aboslute . Mostly the governing punching load is

Note: For determination of punching load from columns are used original internal forces from FEM analysis (not the recalculated ones).

Steel fibre reinforced concrete plate

Each calculated node for punching design has to have a reference on some 2D member. In many case, the region around the node also includes other 2D members with even different properties than the referenced plate. To overcome that issue, a homogenization of properties of the relevant plates is done in advance to prepare required input data for punching design. Two following procedures are performed. Firstly, to get unified outer boundary of plates per a floor, all the connected plates lying in the common plane (same as the referenced plate) are virtually merged together. From the merging procedure are automatically excluded plates with a different type or material than the referenced plate. Secondly, within the unified boundary is created around each calculated node a circular region of radius 3h + a, where h is thickness of the referenced plate of the node and a is half-width of the loaded area. Required input data for punching design are than extracted and homogenized from mesh nodes / elements within this region as follows:

• Ceiling / Foundation - if plate is supported by surface support (contact stresses is present on all mesh nodes / elements in the region) than the plate is assumed as foundation, else ceiling plate is considered
• Thickness (h) - taken as minimum value recognized from all mesh nodes / elements in the region
• Material (f_cd) - taken as minimum value recognized from all mesh nodes / elements in the region

Note: If the properties of a plate around the node are not constant (some homogenization is required), user is informed about that fact by notes via E/W/N system.

Longitudinal reinforcement

Same region like for the recognizing of steel fibre concrete plate properties is assumed for evaluation of longitudinal reinforcement coming to the punching design. As a source a user practical longitudinal reinforcement is used. The following characteristics are calculated:

• Effective depth (d_eff) - there can be distinguish two cases based on longitudinal reinforcement existence on the slab
  • with standard longitudinal reinforcement - taken as minimum value from effective depths (d_eff,i) of mesh nodes / elements within the region calculated according to formula:

  d_eff,i = (d_y,i+d_z,i) / 2

  • without standard longitudinal reinforcement - taken as entire height of the slab

d = h

• Reinforcement ratio (ρ_l) - taken as mean value from reinforcement ratios (ρ_l,i) of mesh nodes / elements within the region calculated according to formula:

ρ_l,i = √(ρ_y,i.ρ_z,i) where

ρ_y,i = A_sy,i / (b*d_y,i) and ρ_z,i = A_sz,i / (b*d_z,i)

Punching design procedure

Basic control perimeter

If the load transfer is non-uniform (due to unbalanced bending moments), local peak loading should be compensated with the help of a lump-sum factor β for V_Ed. For structures where the lateral stability does not depend on frame action between the slabs and the columns, and where the adjacent spans do not differ in length by more than 25%, approximate values for β may be used. The user must decide whether these approximate values can be used, because the program cannot check the preconditions described above.

Approximate values of β for use in a specific country may be found in settings for Concrete National Annex.

Punching shear force

The design procedure for punching shear is based first of all on checks at the face of the column u₀ and at the basic control perimeter u₁. The maximum shear stress is calculated for considered control perimeter u_i according clause 6.4.3(1) as follows:

v_Ed,ui = β ∙ |V_Ed| / (u_i ∙ d_eff)

where

β_l is factor ...

 

Punching resistance with fibres and without shear reinforcement

The effect of the steel fibres in punching check is, similarly in shear check, covered by additional component (v_Rd,cf) in equation for calculation of overall cross-section resistance (v^f_Rd,c) as follows

v^f_Rd,c = min ( v_Rd,c + v_Rd,cf; 1,4 . v_Rd,c)

Where the punching shear resistance( v_Rd,c) of a plate is checked at the basic control perimeter according clause 6.4.4(1) as follows:

v_Rd,c = C_Rd,c ∙ k ∙ (100 ∙ ρ_l∙ f_ck)^1/3 + k₁.s_cp≥ v_min

where

C_Rd,c = 0.18 / γ_c

k = 1 + √(200 / d_eff) ≤ 2.0 where d_eff in [mm]

ρ_l is average reinforcement ratio in specific distance around column

f_ck is characteristic concrete compressive strength in [MPa]

v_min = 0.035 ∙ k^3/2 ∙ f_ck^1/2

k₁ = 0,1; this value is NA dependent

s_cp - normal concrete stress taken into account as difference of shear forces in the columns

 

and contribution of fibre in resistance v_Rd,cf

v_Rd,cf = 0,85 . a^f_c . f^f_ctR,u / g^f_ct

where

a^f_c reduction factor which is aligned with the design concept of this document to allow for long-term effects on the residual tensile strength of steel fibre reinforced concrete (see [1] DAfStb Guideline "Steel fibre reinforced concrete"); default = 0,85

g^f_ct- partial safety factor according to Table R.1 (see [1] DAfStb Guideline "Steel fibre reinforced concrete"); default = 1,25

f^f_ctR,u - residual value of steel fibre reinforced concrete

The calculation of f^f_ctR,u is dependent on member size factor (k^f_G) . This factor is during punching calculated as follows:

 

k^f_G = 1+ A^f_ct.0,5≤1,7

where

A^f_ct = u₁.d

 

The following condition must be satisfied to avoid necessity of punching shear reinforcement:

UC_vfRd,c = v_Ed,u1 / v^f_Rd,c ≤ 1.0

When this condition is not fulfilled, the warning W6/102 occurs and design of shear reinforcement continues (with final status OK, but to indicate that shear reinforcement is required).

Beside that, at the column perimeter, the maximum punching shear stress is checked according to clause 6.4.5(3) as follows:

v_Rd,max = 0.4∙ v ∙fcd

See NA values in Theoretical Background - National annexes to EN1992

As a result, he following condition must be satisfied to keep the plate designable

UC_vRd,max = v_Ed,u0 / v_Rd,max ≤ 1.0

When this condition is not fulfilled, the warning W6/101 occurs and design procedure ends with status Not OK.

As a summary, when the shear reinforcement is not required, the final unity check value is calculated as follows:

UC = max {UC_vfRd,c; UC_vRd,max}

 

Design of shear reinforcement

If punching reinforcement is required, the outer control perimeter u_out beyond which the reinforcement is no longer needed is calculated acc. to clause 6.4.5(4)

u_out = β ∙ |V_Ed| / (v_Rd,c ∙ d_eff)

Be aware in case of shear reinforcement is required then fibre contribution is not allowed to consider (see Re 6.4.5 [1] DAfStb Guideline "Steel fibre reinforced concrete"). Thus shear resistance of concrete only is mentioned in the formula below.

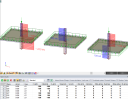
A shape of outer control perimeter is searched iteratively to find a distance, a_out, for which the outer control perimeter has the necessary length. I The shape of the outer control perimeter is considered same as for the basic control perimeter. In some cases, this condition cannot be fulfilled and different shape is used (see warning W6/113). If any outer perimeter with required length cannot be constructed, the design procedure cannot be done successfully (see error E6/106). If any opening is near the loaded area, the reduction of the outer perimeter is considered, which leads to increasing of value a_out.

[fig. - different shape of uout] [fig. - problem to find uout]

Distribution of shear reinforcement

Within the u_out, the shear reinforcement is designed using the following assumptions:

• the distribution of the shear links is considered only as radial
• just vertical shear links are supported
• the shape of reinforcement perimeters around the column is used same as basic control perimeter

TODO: Settings for distribution of shear reinforcement and diameter of shear links

The required area A_sw,reqof one perimeter of shear reinforcement around the column assumed as radially distributed vertical shear links is calculated as

A_sw,req =[(v_Ed,u1 - 0.75 ∙ v_Rd,c) ∙ u₁ ∙ s_r] / (1.5 ∙ f_ywd,ef)

where

f_ywd,ef is effective design strength of the punching reinforcement acc. to formula:

f_ywd,ef= 200 + 0.25 ∙ d_eff ≤ f_ywd

TODO: Settings for distribution of shear reinforcement and diameter of shear links

The required area is further adjusted to fulfil detailing provision rules acc. to clause 9.4.3(1), so that number of shear links n_s per each reinforcement perimeter is following (rounded up)

n_s= max { 4 ∙ A_sw,req/ (π ∙ d_s²); u_1,last / s_t,max,u1; u_s,last / s_t,max,out }

where

d_s is diameter of shear link

u_1,last / s_t,max,u1 represents condition of maximum allowed tangential spacing of links of reinforcement perimeters placed within the basic control perimeter (u_1,last is length of last perimeter of shear reinforcement there)

u_s,last / s_t,max,out represents condition of maximum allowed tangential spacing of links of reinforcement perimeters placed outside the basic control perimeter (u_s,last is length of last perimeter of shear reinforcement there)

Note: Settings for detailing rules...

The last condition, which must be fulfilled acc. to clause 9.4.3(2) is minimum reinforcement area of single shear link A_sw1,min acc. to formula

A_sw1,min = 0.08 ∙ √ ( f_ck / f_ywk) ∙ s_r ∙ s_t / 1.5

where

s_t is tangential spacing of shear links of last perimeter of shear reinforcement around column

[fig. Asw1min + st]

The final designed area of each perimeter of shear reinforcement around the column is than as follows

A_sw = n_s ∙ π ∙ d_s² / 4 ≥ n_s ∙ A_sw1,min

where condition about minimum reinforcement area of shear link is automatically checked and design is recalculated with an increment of n_s if the condition is not satisfied.

[fig. ns + ds] [fig setup for ds]

The required number of shear reinforcement perimeters around column, n_per, is determined based on clause 6.4.5(4), which specifies that the outermost perimeter of shear reinforcement, a_s,last = s₀ + s_r ∙ n_per, should be placed at a distance not greater than k_out ∙ d_eff within u_out. The following formula for n_per is derived

n_per = [(a_out - s₀ - k_out ∙ d_eff) / s_r] + 1 ≥ n_per,min

where

k_out is coefficient to determine the maximum distance of last perimeter from u_out

n_per,min is minimum number of reinforcement perimeters around column required acc. to clause 9.4.3(1)

Note: The coefficient kout is National Annex value and can be edited using Concrete Setup.

The total amount of shear reinforcement A_sw,tot around the column is than simply calculated as

A_sw,tot = n_per ∙ A_sw

[fig Asw,tot]

 

Punching resistance with shear reinforcement

To confirm, that designed amount of shear reinforcement is sufficient, the punching resistance of a plate with shear reinforcement is verified in required number of control perimeters, n_c,per, as follows

n_c,per = [s₀ + (n_per - 1) ∙ s_r] / a_u1

where

a_u1 = 2 ∙ d_eff and represents the equidistant spacing of control perimeters from column face

The shape of control perimeters is primarily considered same as for the basic control perimeter. However, it it's not possible to construct it in same pattern due to the plate boundary, than different shape pattern with minimised length is used instead (see warning W6/118).

[fig. TODO]

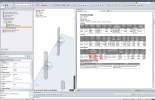
Note: All control perimeters used during the punching design procedure can be displayed in the graphical window to be checked also visually.

The punching resistance with shear reinforcement is calculated for i-th control perimeter using expression in clause 6.4.5(1)

v_Rd,cs,i = 0.75 ∙ v_Rd,c + 1.5 ∙ (d_eff / s_r) ∙ A_sw ∙ f_ywd,ef / (u_i ∙ d_eff) ≤ k_max ∙ v_Rd,c

where

u_i is lenght of i-th control perimeter with the distance from column face a_ui = i * 2 * d_eff

The maximum capacity that can be achieved by application of shear reinforcement is limited by the value k_max∙v_Rd,c according to clause 6.4.5(1). Hence, the unity check of the punching resistance with shear reinforcement can be formulated as

UC_vRd,cs = max {v_Ed,ui / v_Rd,cs,i; v_Ed,ui / (k_max ∙ v_Rd,c)} ≤ 1.0

It's obvious, that due to this limitation not always can be shear reinforcement successfully designed (see warning W6/117). In such case, it's recommended to increase

Note: The factor kmax is National Annex value and can be edited via Concrete Setup.

To be sure, that all detailing rules related to punching reinforcement are fulfilled,